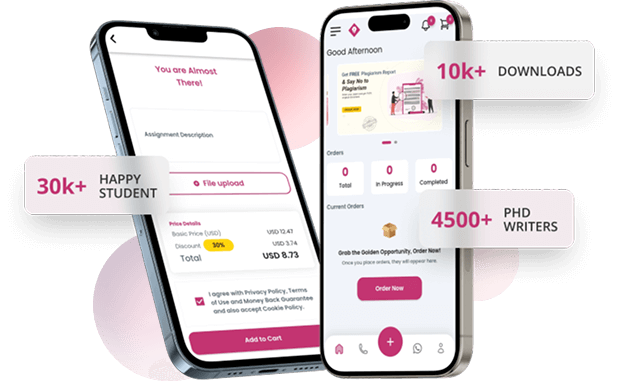
-
Services
- Back
-
Assignment Services
Back Assignment Services
- Conclusion Writing Service
- Cheap Assignment Help
- Custom Assignment
- Do My Assignment
- University Assignment
- Assignment Editing Services
- ATHE Assignment
- BTEC Assignment
- CTH Assignment
- HND Assignment
- Last Minute Assignment
- Make My Assignment
- Solve My Assignment
- Urgent assignment
- Management Assignment
- High School Assignment
- Assignment Proofreading Service
- Assignment Writing Tips
- Resume Writing Help
- Academic Writing Service
- Global Assignment Help
- My Assignment Help
- Ghost Writer
- Open Book Exam
- Report Writing
- Personal Statement Writing Service
- Write My Assignment
- Assignment Expert
- Online Exam Help
- Exam Tips
- Essay Writing Help
-
Dissertation Help
Back Dissertation Help
- Marketing
- Business Dissertation Topics
- Finance Dissertation Topics
- Economics Dissertation Topics
- Psychology Dissertation Topics
- MBA Dissertation Topics
- History Dissertation Topics
- Nursing Dissertation Topics
- Management Dissertation Topics
- Accounting Dissertation Topics
- Fashion Dissertation Topics
- English Dissertation Topics
- Human Resource Dissertation Topics
- Tourism Dissertation Topics
- Computer Science Dissertation Topics
- Media Dissertation Topics
- Politics Dissertation Topics
- E-Commerce Dissertation Topics
- Operations Management Dissertation Topics
- Education
- PhD Dissertation
- Engineering Dissertation
- Academic Dissertation
- Biology Dissertation
- Psychology Dissertation
- Statistics Dissertation
- Law Dissertation
- Marketing Dissertation
- MBA Dissertation
- Nursing Dissertation
- Finance Dissertation
- Write My Dissertation
- Dissertation Help London
- Dissertation Help Manchester
- Dissertation Structure
- Dissertation Proofreading Services
- Dissertation Conclusion
- Dissertation Editing Services
- Masters Dissertation Help
- Dissertation Proposal
- Dissertation Writing Services
- Dissertation Format
- Coursework Help
- Do My Homework
-
Assignment Subjects
Back Assignment Subjects
- Accounting
- Business
- Calculus
- Computer Science
- Culture
- Chemistry
- English
- Epidemiology
- Employee Motivation
- Economics
- Entrepreneurship
- Finance
- Fashion
- Financial Accounting
- Geometry
- Game Theory
- Geography
- History
- Human Resources
- Hospitality
- Maths
- MBA
- Media
- Marketing
- Mass Communication
- Micro Economics
- Music
- Medical Education
- Tourism
- Nursing
- Probability
- Psychology
- Science
- SPSS
- Statistics
- Physics
- Biology
- Architecture
- Sociology
- Philosophy
- Public Economics
- Taxation
- Childcare
- Bio Mechanics
- Web Designing
- Anatomy
- Business Environment
- Strategy
- Business Decision Making
- Public Relations
- Behavioral Finance
- Organization Development
- Leadership
- Industrial Marketing
- Biotechnology
- Biometry
- Trigonometry
- Training Assignment Help
- Countries
- Cities
- Case Study
- Resources
- Hire Writers
- Blogs
- Academic Tools
Popular Search
Login
0-

-
Services
- Back
-
Assignment Services
Back Assignment Services
- Conclusion Writing Service
- Cheap Assignment Help
- Custom Assignment
- Do My Assignment
- University Assignment
- Assignment Editing Services
- ATHE Assignment
- BTEC Assignment
- CTH Assignment
- HND Assignment
- Last Minute Assignment
- Make My Assignment
- Solve My Assignment
- Urgent assignment
- Management Assignment
- High School Assignment
- Assignment Proofreading Service
- Assignment Writing Tips
- Resume Writing Help
- Academic Writing Service
- Global Assignment Help
- My Assignment Help
- Ghost Writer
- Open Book Exam
- Report Writing
- Personal Statement Writing Service
- Write My Assignment
- Assignment Expert
- Online Exam Help
- Exam Tips
- Essay Writing Help
-
Dissertation Help
Back Dissertation Help
- Marketing
- Business Dissertation Topics
- Finance Dissertation Topics
- Economics Dissertation Topics
- Psychology Dissertation Topics
- MBA Dissertation Topics
- History Dissertation Topics
- Nursing Dissertation Topics
- Management Dissertation Topics
- Accounting Dissertation Topics
- Fashion Dissertation Topics
- English Dissertation Topics
- Human Resource Dissertation Topics
- Tourism Dissertation Topics
- Computer Science Dissertation Topics
- Media Dissertation Topics
- Politics Dissertation Topics
- E-Commerce Dissertation Topics
- Operations Management Dissertation Topics
- Education
- PhD Dissertation
- Engineering Dissertation
- Academic Dissertation
- Biology Dissertation
- Psychology Dissertation
- Statistics Dissertation
- Law Dissertation
- Marketing Dissertation
- MBA Dissertation
- Nursing Dissertation
- Finance Dissertation
- Write My Dissertation
- Dissertation Help London
- Dissertation Help Manchester
- Dissertation Structure
- Dissertation Proofreading Services
- Dissertation Conclusion
- Dissertation Editing Services
- Masters Dissertation Help
- Dissertation Proposal
- Dissertation Writing Services
- Dissertation Format
- Coursework Help
- Do My Homework
-
Assignment Subjects
Back Assignment Subjects
- Accounting
- Business
- Calculus
- Computer Science
- Culture
- Chemistry
- English
- Epidemiology
- Employee Motivation
- Economics
- Entrepreneurship
- Finance
- Fashion
- Financial Accounting
- Geometry
- Game Theory
- Geography
- History
- Human Resources
- Hospitality
- Maths
- MBA
- Media
- Marketing
- Mass Communication
- Micro Economics
- Music
- Medical Education
- Tourism
- Nursing
- Probability
- Psychology
- Science
- SPSS
- Statistics
- Physics
- Biology
- Architecture
- Sociology
- Philosophy
- Public Economics
- Taxation
- Childcare
- Bio Mechanics
- Web Designing
- Anatomy
- Business Environment
- Strategy
- Business Decision Making
- Public Relations
- Behavioral Finance
- Organization Development
- Leadership
- Industrial Marketing
- Biotechnology
- Biometry
- Trigonometry
- Training Assignment Help
- Countries
- Cities
- Case Study
- Resources
- Hire Writers
- Blogs
- Academic Tools
- Order Now